Övergången från abakus till dagens räknare var långsam, men däremellan fanns uppfinningar som ”Napiers ben” som revolutionerade tillgången till komplex matematik.
Namnet John Napier säger dig kanske ingenting, men jag kan lova dig att du troligen inte gillar honom. För det du kanske känner till är logaritmer, som gjorde så många av oss galna i gymnasiet. Det var Napier som först definierade denna funktion, men för att ”kompensera” skapade han också det som kan betraktas som föregångaren till dagens miniräknare.
Något som kallas ”Napiers ben” och som ser ut som domino, men som gjorde matematiska operationer tillgängliga för fler människor.
John Napier.

Denna skotte var intresserad av många saker. Hans familj var välbärgad och som en god son gick han på Saint Andrews University vid 13 års ålder. Det varade inte länge, men inte för att han ville sluta studera, utan för att han gick till andra universitet i Frankrike, Italien och Flandern. Han tillbringade sitt liv på olika slott, där han gav fritt utlopp för flera av sina passioner.
En trollkarl (men inte med siffror). Han var protestant och ansågs av sina grannar vara en svart magiker. Han var också en uppfinningsrik person. När duvorna åt upp hans säd beslöt han att sprida frön doppade i alkohol över fältet och, när duvorna var ”bedövade” och oförmögna att flyga, ägnade han sig åt att fånga dem. Som alltid, och särskilt när vi talar om denna typ av historier med flera århundraden på nacken, gör fantasin och överdrifterna sitt, men det är oundvikligt att Napier gillade att lösa problem.
Hans största bidrag är det omtalade Mirifici Logarithmorum Canonis Descriptio, där han 1614 definierade de nuvarande logaritmerna, men både före och efter publicerade han andra avhandlingar inom matematik där han utforskade sätt att förenkla beräkningar. Han teoretiserade inte bara om dem eller främjade decimaltecknet: han skapade verktyg för att lösa dessa beräkningar på ett enklare sätt.
Den nya abakusen.

Sedan vi började lösa matematiska problem har mänskligheten letat efter sätt att använda verktyg. Så uppstod abakusen, eller quipus, med vilka man kunde utföra enkla operationer som addition, subtraktion och multiplikation. Med mer komplex matematik var det nödvändigt att omarbeta systemet, och Napier tog fram sin nya abakus, eller en prototyp till en kalkylator.
Napiers ben.
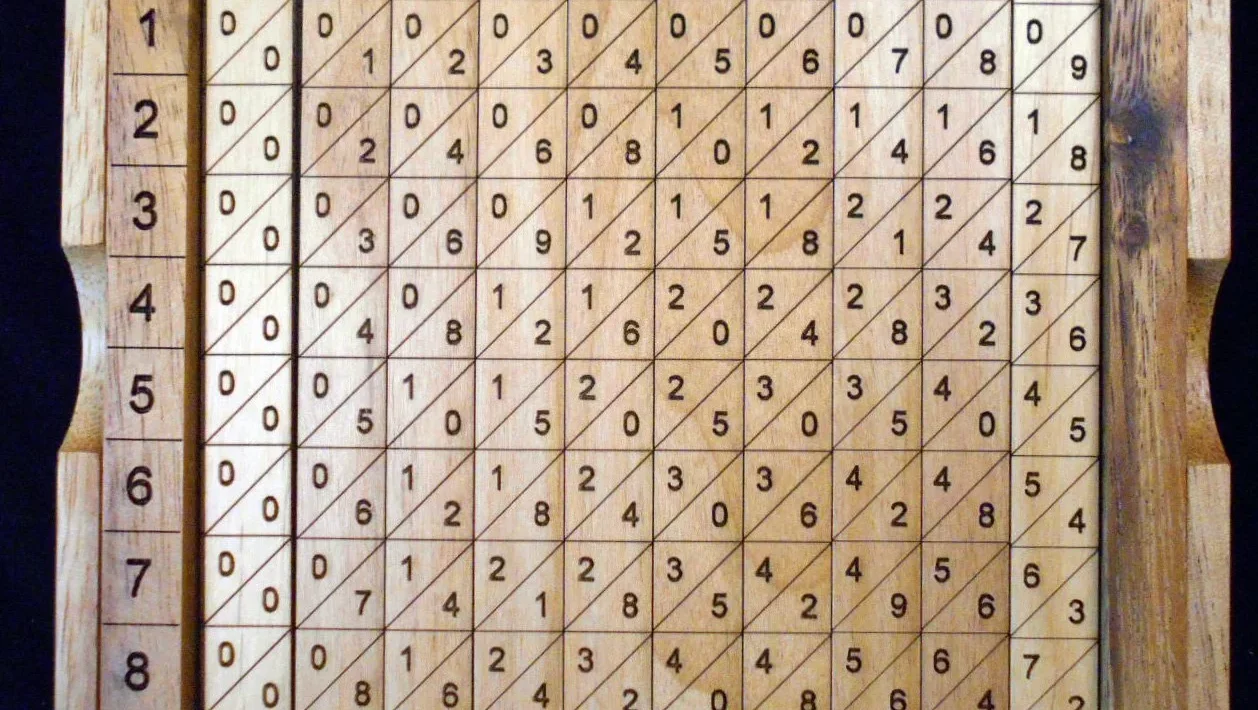
1617, kort före sin död, uppfann matematikern ett manuellt verktyg som skulle underlätta vissa mer komplexa operationer, såsom multiplikation och division, men också kvadratrötter. Det var en uppsättning rektangulära stavar på vilka multiplikationstabellerna var ingraverade, samt en tavla med hål för stavarna och siffrorna 1 till 9 placerade vertikalt på vänster sida.

Genom att placera dessa stavar bredvid varandra reducerades multiplikations- och divisionsoperationerna till enkla additioner respektive subtraktioner. Ursprungligen tillverkades de främst av metall eller trä, men stavarna kunde också tillverkas av elfenben, och ett komplett set innehöll 10 stavar för att representera siffrorna 0 till 9.
Vad?
Okej, som med matematik, låt oss titta på några exempel. Ett mycket enkelt exempel är multiplikation, eftersom vi då inte behöver memorera tabellerna. Om vi vill veta hur mycket 2 x 6 är, letar vi bara upp rad 2 till höger och pinnen som börjar med 6 och ser vilket tal som finns i kvadranten: 12. Om vi vill räkna 8 x 8 upprepar vi processen och ser att vi får 64.
Om vi gör en mer komplex operation, som 46785399 x 7, placerar vi stavarna som motsvarar det talet (den som börjar med 4, den som börjar med 6 och så vidare) bredvid varandra från vänster till höger och tittar på siffran som visas i rad 7, som är den vi vill multiplicera med.
Nu placerar vi siffrorna som visas tillsammans i det diagonala fältet från höger till vänster: 327497793. Senare matematiker förbättrade systemet genom att skapa en tavla med en lutning på 65º som förbättrade den visuella identifieringen av formeln, men ”Napiers ben” var en revolution som gjorde denna komplexa matematiska beräkning tillgänglig för personer utan högre utbildning. Det enda man behövde lära sig var multiplikations- och divisionsregeln med tavelsystemet.
En juvel.
Napier dog 1617, så det är svårt att säga om han insåg betydelsen av sitt verk, både teoretiskt och praktiskt, men idag används fortfarande hans logaritmiska grunder, liksom decimaltecknet, en månekrater är uppkallad efter honom och den neperianska abakusen är en av juvelerna i Arkeologiska museet i Madrid.

Det är okänt vem som tillverkade den, men det är en träask av ansenlig storlek med 30 lådor där brickorna från de två abakusar som matematikern designade förvaras. Den ena består av 60 numrerade stavar av ben och den andra, kallad ”promptuario”, består av 300 numrerade och perforerade brickor av ull för att utföra multiplikationer.
Och det är som en megachuleta, eftersom på lådornas luckor finns de första potenserna av siffrorna, koefficienterna för de första potenserna av binomen och de numeriska uppgifterna för de regelbundna polyedrarna. Det är intressant att miniräknare, förutom att vara föremål med ett specifikt syfte, i vissa fall har blivit verkliga konstverk. Fråga Divisumma.